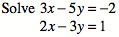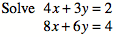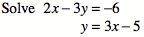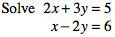Search Results
Math Topics
High School Algebra 2
*Systems of Equations
1
Systems of Linear Equations in Two Variables
Mini Lecture
Solve:
\[\begin{aligned} 3x-5y &= -2\\ 2x-3y &= 1\end{aligned}\]
\[\begin{aligned} 4x-3y &= 2\\ 8x-6y &= 4\end{aligned}\]
\[\begin{aligned} \dfrac{1}{2}x-\dfrac{1}{3}y &= 2\\ \dfrac{1}{4}x+\dfrac{2}{3}y &= 6\end{aligned}\]
\[\begin{aligned} 2x-3y &= 2\\ y &= 3x-5\end{aligned}\]
2
Systems of Linear Equations in Three Variables
3
Introduction to Determinants
4
Cramer's Rule
5
Matrix Solutions to Linear Systems
6
Applications and Modeling
If water at room temperature is \(77^{\circ}F\) or \(25^{\circ}C\). And the water boils at \(212^{\circ}F\) or \(100^{\circ}C\). Assume the relationship between the two scales is linear, find the formula that gives the Celsius temperature \(C\) in terms of Fahrenheit temperature \(F\).
7
Inequalities and Systems of Inequalities in Two Variables

A basketball arena charges \(\$20\) for certain seats and \(\$15\) for others. They want to make more than \(\$18,000\) and reserve at least \(500\) \(\$15\) seats. Find the system of inequalities and sketch the graph. If \(620\) tickets are sold for \(\$15\), at least how many are sold for \(\$20\)?